1. 개요
연결 리스트는 "노드" 에 객체를 담고, 포인터를 통해 연결되어있다.
단일 연결 리스트는 next 포인터로 앞으로 밖에 갈 수 없지만, 이중 연결 리스트는 prev, next 포인터
가 있어서 뒤로도 갈 수 있다.
단일 연결 리스트로 가장 마지막에 데이터를 넣으려면 처음부터 포인터를 타고 가야 하므로, 데이터가
100개면 100번, 1억개면 1억번 이동을 해야 하는데
이중 연결 리스트는 마지막에 tail이라는 더미 노드를 만들어놓고, 뒤로 갈 수 있기에, tail 에서 prev
포인터로 이동하면 데이터가 100만개가 있던, 1억개가 있던 1번의 동작으로 그 위치까지 이동할 수 있다.
또한, 삽입이나 삭제를 할 때도, head와 tail중, 가까운 곳에서 탐색을 시작하면, 데이터가 100만개면
최대 50만번, 1억개면 최대 5000만번의 이동으로 원하는 위치로 이동할 수 있다.
단점으로는 포인터를 2개 가지므로, 그만큼 메모리가 소비되며, 구현이 살짝 더 복잡해진다.
2. 구현
package list;
public interface IList<T> {
void add(T t);
void insert(int index, T t);
void clear();
boolean delete(T t);
boolean deleteByIndex(int index);
T get(int index);
int indexOf(T t);
boolean isEmpty();
boolean contains(T t);
int size();
}
package list;
public class MyDoubleLinkedList<T> implements IList<T> {
private Node head;
private Node tail;
private int size;
public MyDoubleLinkedList() {
this.size = 0;
this.head = new Node(null);
this.tail = new Node(null);
this.head.next = this.tail;
this.tail.prev = this.head;
}
@Override
public void add(T t) {
Node last = this.tail.prev;
Node node = new Node(t, last, tail);
last.next = node;
this.tail.prev = node;
this.size++;
}
@Override
public void insert(int index, T t) {
if (index >= this.size || index < 0) {
throw new IndexOutOfBoundsException();
}
Node prev = null;
Node curr = null;
int i = 0;
if (index < this.size / 2) {
prev = this.head;
curr = this.head.next;
while (i++ < index) {
prev = prev.next;
curr = curr.next;
}
} else {
curr = this.tail;
prev = this.tail.prev;
while (i++ < (this.size - index)) {
curr = curr.prev;
prev = prev.prev;
}
}
Node node = new Node(t, prev, curr);
prev.next = node;
curr.prev = node;
this.size++;
}
@Override
public void clear() {
this.size = 0;
this.head.prev = null;
this.head.next = this.tail;
this.tail.prev = this.head;
this.tail.next = null;
}
@Override
public boolean delete(T t) {
Node prev = this.head;
Node curr = prev.next;
for (int i = 0; i < this.size; i++) {
if (curr.data.equals(t)) {
prev.next = curr.next;
curr.next.prev = prev;
curr.prev = null;
curr.next = null;
this.size--;
return true;
}
prev = prev.next;
curr = curr.next;
}
return false;
}
@Override
public boolean deleteByIndex(int index) {
Node prev = null;
Node curr = null;
Node next = null;
int i = 0;
if (index < this.size / 2) {
prev = this.head;
curr = this.head.next;
while (i++ < index) {
prev = prev.next;
curr = curr.next; // curr에 지우고 싶은 데이터가 들어감
}
prev.next = curr.next;
curr.next.prev = prev; // 원래 curr을 가르킴
curr.next = null;
curr.prev = null;
} else { // tail 에서 역으로 찾아가는 경우
curr = this.tail.prev;
next = this.tail;
while (i++ < (this.size - index - 1)) { // 데이터가 있는 노드부터 시작해야 하니 -1
next = next.prev;
curr = curr.prev;
}
next.prev = curr.prev;
curr.prev.next = next;
curr.next = null;
curr.prev = null;
}
this.size--;
return false;
}
@Override
public T get(int index) {
if (index >= this.size || index < 0) {
throw new IndexOutOfBoundsException();
}
int i = 0;
Node curr = null;
if (index < this.size / 2) { // index가 head에서 더 가까우면
curr = this.head.next;
while (i++ < index) {
curr = curr.next;
}
} else { // index가 tail에서 더 가까우면
curr = this.tail.prev;
while (i++ < (this.size - index - 1)) {
curr = curr.prev;
}
}
return curr.data;
}
@Override
public int indexOf(T t) {
Node curr = head;
for (int i = 0; i < this.size; i++) {
curr = curr.next;
if (curr.data != null && curr.data.equals(t)) {
return i;
}
}
return -1;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
@Override
public boolean contains(T t) { // O(N) -> O(N/2)
Node head_curr = this.head.next;
Node tail_curr = this.tail.prev;
while (head_curr == tail_curr || head_curr.prev == tail_curr.next) {
if (head_curr.data.equals(t) || tail_curr.data.equals(t)) {
return true;
}
head_curr = head_curr.next;
tail_curr = tail_curr.prev;
}
return false;
}
@Override
public int size() {
return this.size;
}
private class Node {
T data;
Node prev;
Node next;
Node(T data) { this.data = data;}
Node(T data, Node prev, Node next) {
this.data = data;
this.prev = prev;
this.next = next;
}
}
}
3. 설명
1. 노드 구성
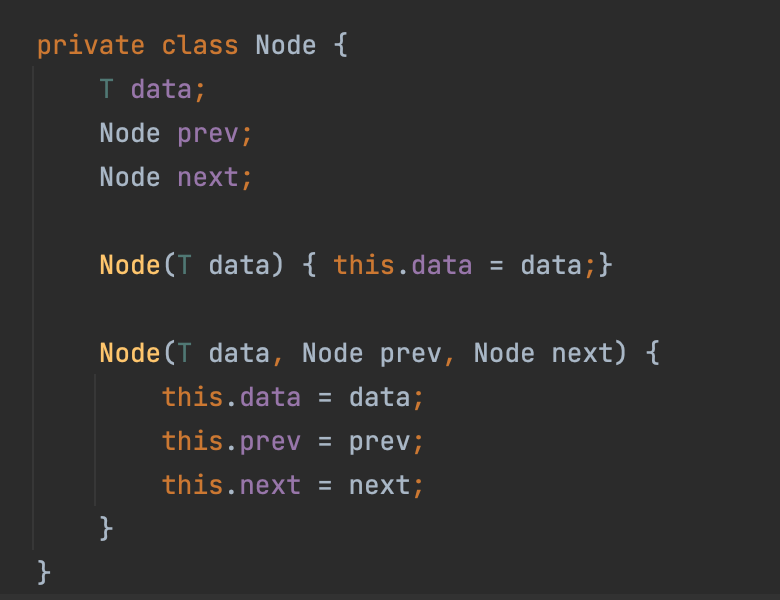
코드의 마지막 부분을 보면 노드가 있을 것이다.
데이터를 담을 data, 이전 노드를 가르키는 prev, 다음 노드를 가르키는 next,
생성 시, 데이터를 넣으면 데이터가 들어가고, 데이터와 포인터를 넣으면 다 삽입되는 노드다.
2. 멤버변수

더미 노드 (데이터가 들어가있진 않지만, 이용을 편리하게 해줄 노드) 인 head와 tail, 리스트의 크기를 나타내는
사이즈가 있다.
3. 생성자
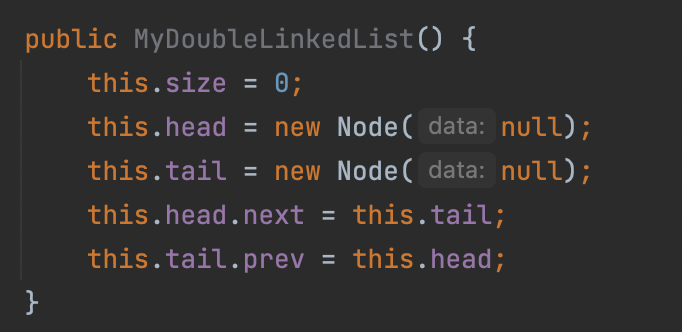
처음 만들 때, 데이터가 들어간 노드는 없으니 사이즈는 0, 헤드와 테일은 Null로 초기화,
head의 next를 테일, tail의 Prev를 head로 설정한다.
4. add(T t)

데이터가 있는 마지막 노드 뒤에 데이터를 삽입하는 메소드다.
데이터를 넣기 위해, 테일 바로 뒤에 Last라는 노드를 생성한다.
그리고 집어넣을 노드에, 데이터로 t를 집어넣고, prev는 last, next는 tail로 설정한다.
last의 next를 새로운 노드로, tail의 prev를 새로운 노드로 설정하는 것으로, 새로운 노드를 연결할 수 있다.
혹시라도 포인터 잘못설정하면 데이터 다 날아가니 조심해야 한다.
5. insert(int index, T t)
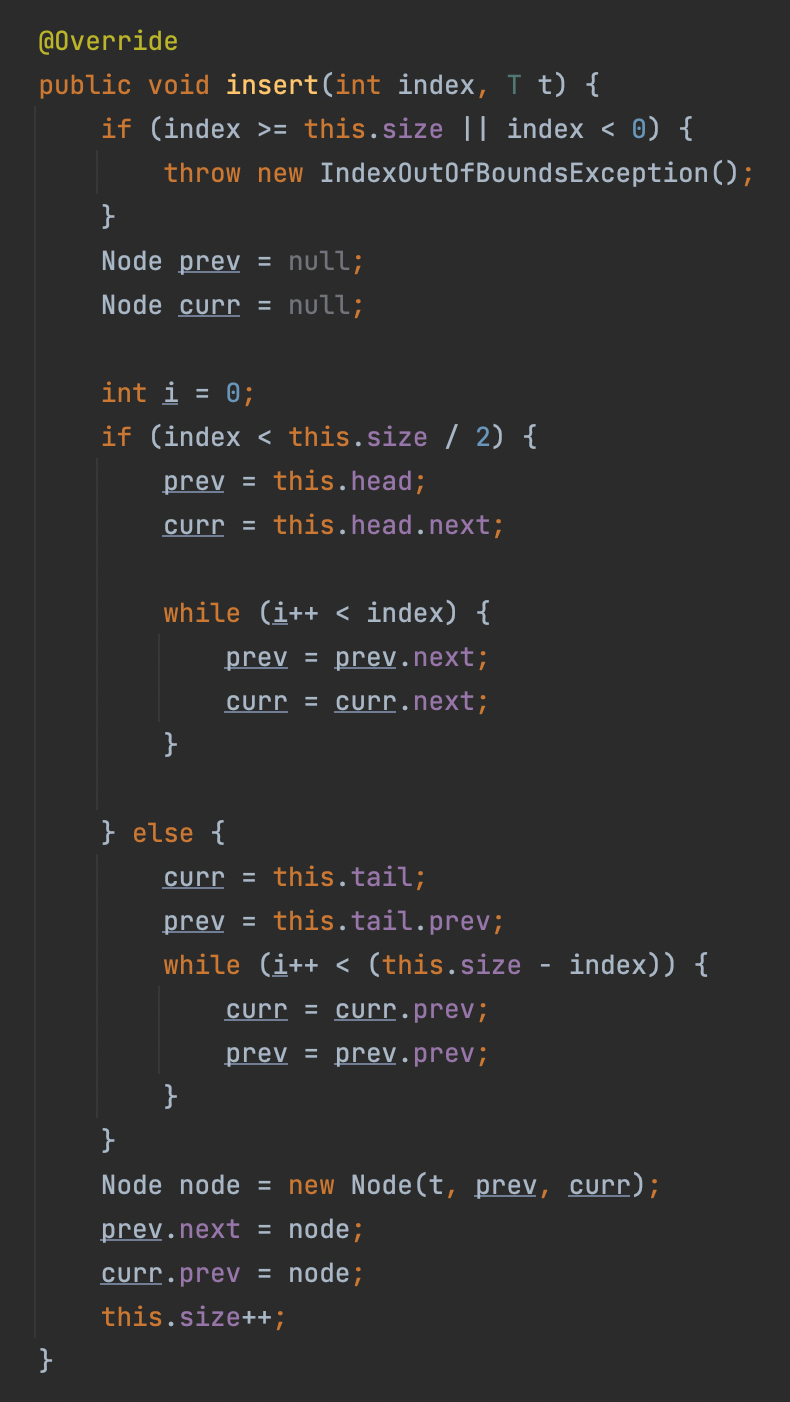
원하는 위치에 t를 집어넣는 메소드다.
만약 인덱스가 사이즈보다 크거나, 같고, 음수라면 에러를 일으킨다.
우선 데이터 변환용으로 prev와 curr이라는 노드를 만들어놓는다.
인덱스가 사이즈의 1/2보다 작다는 말은, 헤드에 가깝단 말이다.
while문으로 코드를 타고, 인덱스의 크기만큼 이동한다.
else면 tail에 가깝다는 말이니, 테일에서 뒤로 인덱스 크기만큼 이동한다.
사이즈 - 인덱스 면 이동해야하는 숫자가 나온다.
이동이 끝나면, curr에는 데이터를 집어넣을 자리가 나올 것이다.
새로운 node에, 데이터로 t를 넣고, prev앞, curr뒤로 포인터를 설정해 집어넣는다.
prev.next, curr.prev 는 새로운 node로 설정하고, 사이즈를 증가시키면 원하는 위치에 데이터를 추가할 수 있다.
6. clear()

사이즈를 0으로 바꾸고, head의 next를 tail, tail의 prev를 head로 바꾸고, 나머지 포인터를 null로 바꿔주면,
원래 있던 데이터는 아무도 참조하지 않으니, 자바의 GC(Garbage Collector, 쓰레기 수집기)가 수거해간다.
7. delete(T t)
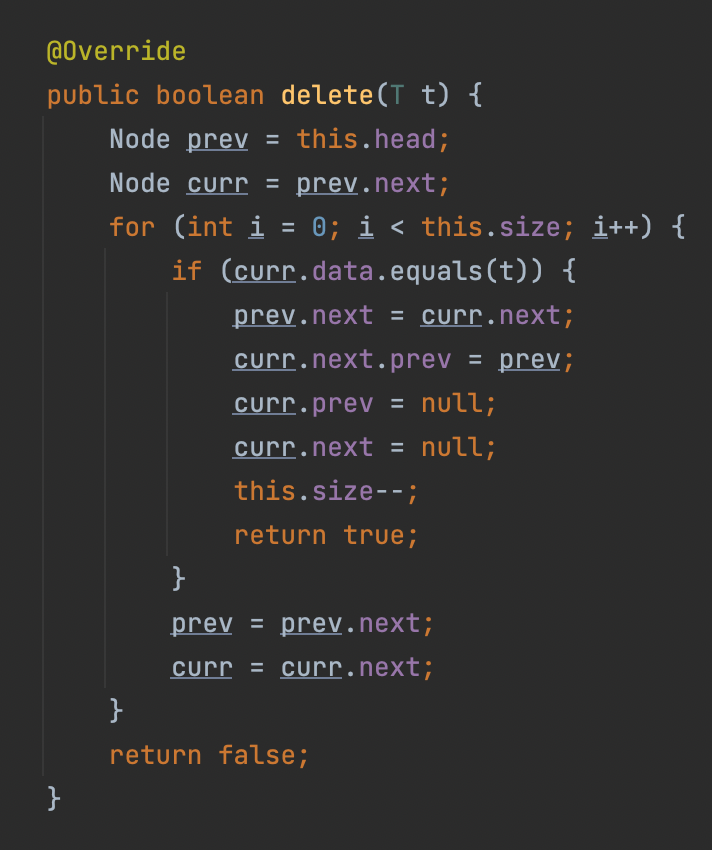
t와 같은 데이터가 있으면 삭제하는 메소드다.
처음부터 사이즈 크기만큼 뒤져보고, t와 같은 데이터를 가진 노드가 있으면, 그 노드의 prev와 next를 지우고,
뒤에 있던 노드의. next를 삭제할 노드 앞에 있는 노드로 바꾸고, 앞에 있던 노드의 prev를 삭제할 노드의
뒤에 있는 노드로 바꿔주고
사이즈를 1 줄이고 삭제에 성공했다고 true를 반환하면 된다.
뒤져보고 없으면 false 반환
8. deleteByIndex(int index)
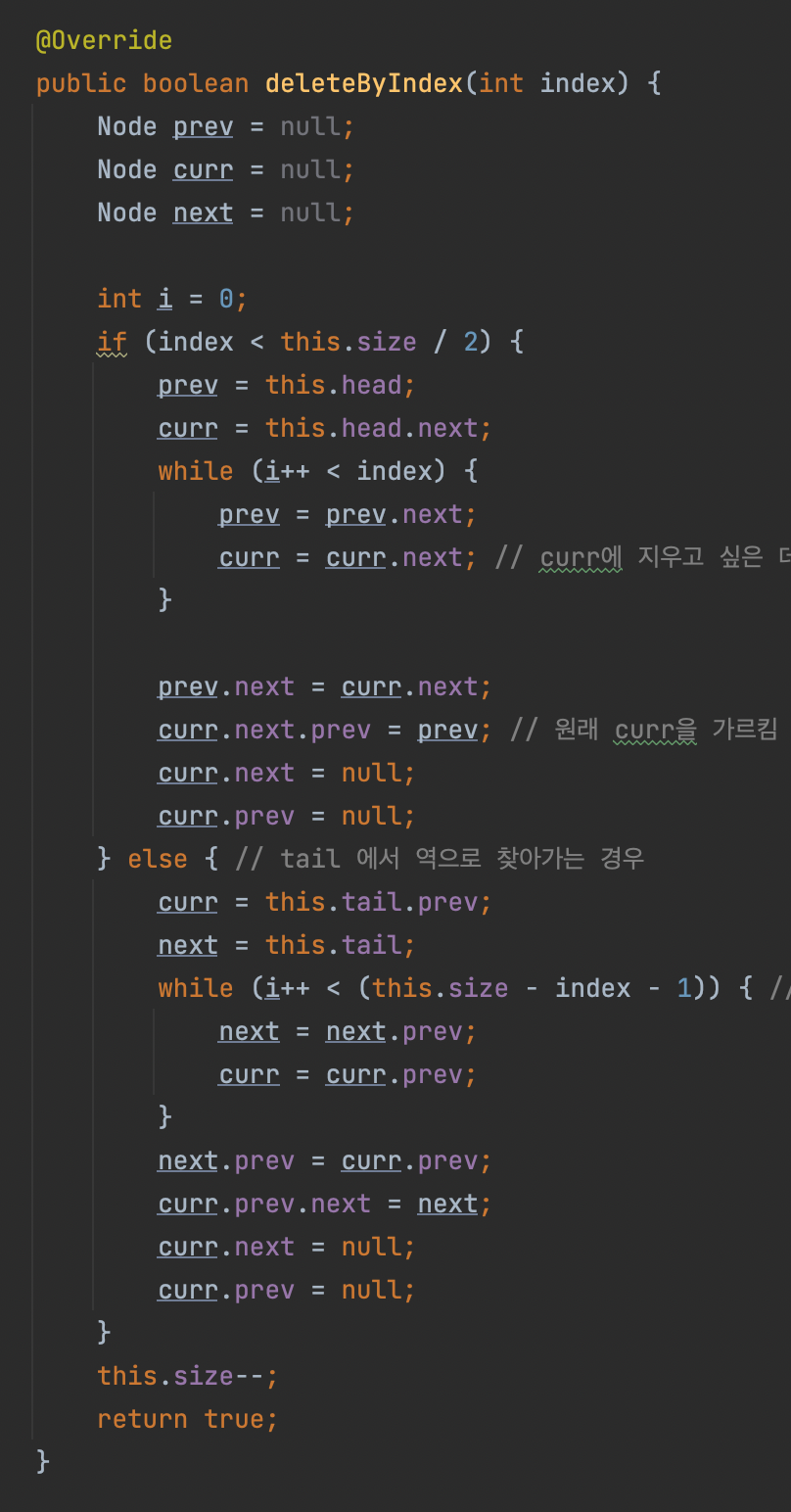
인덱스를 받고, 그 인덱스에 있는 노드를 삭제하는 메소드다.
헤드와 테일, 어디에 가까운지 확인하고 인덱스의 위치로 찾아간다.
그리고 포인터 정리하고, true를 반환한다.
9. T get(int index)
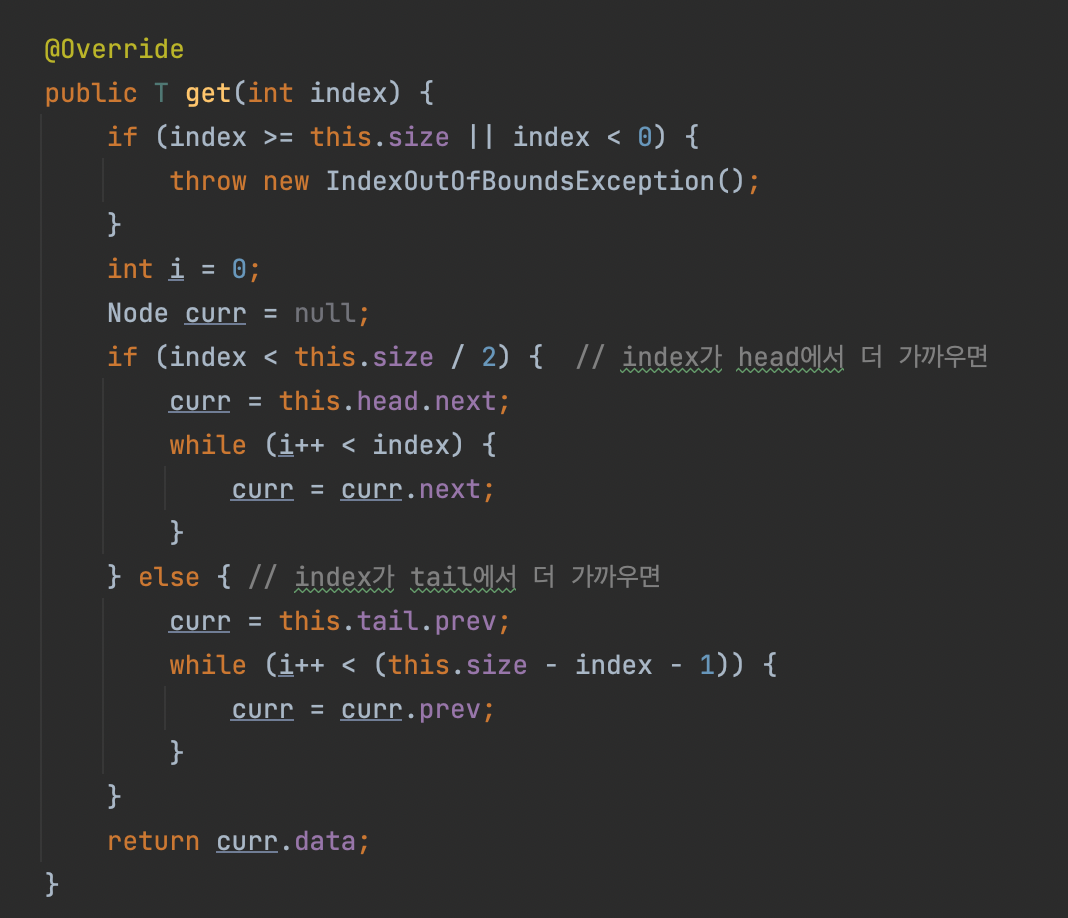
인덱스 위치에 있는 데이터를 반환하는 메소드다.
head와 tail, 어디에서 가까운지 확인하고, 가까운 곳에서 출발해서 그 위치까지 가면, 그 데이터를 return한다.
10. indexOf(T t)

데이터를 처음부터 사이즈 크기만큼 뒤져보고, 같은 게 나오면 그 번호를 반환하는 메소드다.
만약 같은 게 없으면 -1 반환한다.
11. isEmpty()

비었나 확인하는 메소드다.
boolean이니 this.size가 0이면 true, 아니면 false를 반환한다.
12. contains(T t)
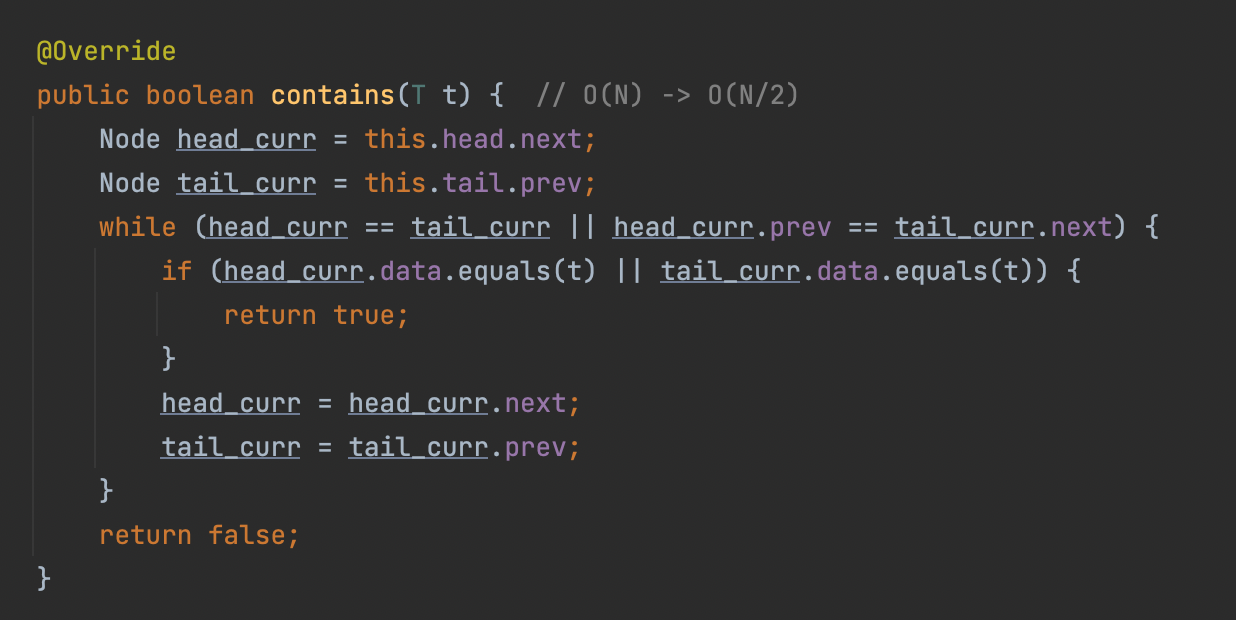
헤드와 테일에서 서로 다가오면서 t와 같은 데이터가 포함되어 있나 확인하는 메소드다.
있으면 true, 없으면 false 반환
13. size()

리스트의 크기를 반환하는 메소드다.
'자료구조' 카테고리의 다른 글
| 자료구조 선형 큐 (Linear Queue) 자바로 구현 (0) | 2022.02.16 |
|---|---|
| 자료구조 스택 (Stack) 자바로 구현 (0) | 2022.02.15 |
| 자료구조 배열 리스트 (ArrayList) 자바로 구현 (0) | 2022.02.13 |
| 자료구조 연결 리스트(Linked List) 자바로 구현 (0) | 2022.02.13 |
| 8주차, 자료구조 연결 리스트(Linked List) (0) | 2022.02.12 |




댓글